1. 평가(Evaluation)
- 머신러닝 프로세스
데이터 가공/변환 - 모델 학습/예측 - 평가
- 성능 평가 지표(Evaluation Metric)는 모델이 회귀인지 분류인지에 따라 나뉨
1) 회귀의 경우 대부분 실제값과 예측값의 오차 평균값에 기반
2) 분류의 평가 방법 -> 이번 장에서배울 내용
분류의 성능평가 지표
- 정확도
- 오차행렬
- 정밀도
- 재현율
- F1 스코어
- ROC AUC
1. 정확도( ACCURACY)
: 실제 데이터에서예측 데이터가 얼마나 같은지 판단하는 지표( 직관적으로 모델 예측 성증 나타내는 지표)
정확도(Accuracy) = 예측 결과가 동일한 데이터 건수 / 전체 예측 데이터 건수
: 특정 결과 값 True가 몰려있고 정답을 무조건 True 로 나오도록 한다면 정확도가 높을 것이다.
(잘못된 평가)
# BaseEstimator 클래스를 상속받아 아무런 학습x
import numpy as np
from sklearn.base import BaseEstimator
class MyDummyClassifier(BaseEstimator):
# fit( ) 메소드는 아무것도 학습하지 않음.
def fit(self, X , y=None):
pass
# predict( ) 메소드는 단순히 Sex feature가 1 이면 0 , 그렇지 않으면 1 로 예측함.
def predict(self, X):
pred = np.zeros( ( X.shape[0], 1 ))
for i in range (X.shape[0]) :
if X['Sex'].iloc[i] == 1:
pred[i] = 0
else :
pred[i] = 1
return pred
import pandas as pd
from sklearn.preprocessing import LabelEncoder
# Null 처리 함수
def fillna(df):
df['Age'].fillna(df['Age'].mean(),inplace=True)
df['Cabin'].fillna('N',inplace=True)
df['Embarked'].fillna('N',inplace=True)
df['Fare'].fillna(0,inplace=True)
return df
# 머신러닝 알고리즘에 불필요한 피처 제거
def drop_features(df):
df.drop(['PassengerId','Name','Ticket'],axis=1,inplace=True)
return df
# 레이블 인코딩 수행.
def format_features(df):
df['Cabin'] = df['Cabin'].str[:1]
features = ['Cabin','Sex','Embarked']
for feature in features:
le = LabelEncoder()
le = le.fit(df[feature])
df[feature] = le.transform(df[feature])
return df
# 앞에서 설정한 Data Preprocessing 함수 호출
def transform_features(df):
df = fillna(df)
df = drop_features(df)
df = format_features(df)
return df
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 원본 데이터를 재로딩, 데이터 가공, 학습데이터/테스트 데이터 분할.
titanic_df = pd.read_csv('C:\/train.csv')
y_titanic_df = titanic_df['Survived']
X_titanic_df= titanic_df.drop('Survived', axis=1)
X_titanic_df = transform_features(X_titanic_df)
X_train, X_test, y_train, y_test=train_test_split(X_titanic_df, y_titanic_df, \
test_size=0.2, random_state=0)
# 위에서 생성한 Dummy Classifier를 이용하여 학습/예측/평가 수행.
myclf = MyDummyClassifier()
myclf.fit(X_train ,y_train)
mypredictions = myclf.predict(X_test)
print('Dummy Classifier의 정확도는: {0:.4f}'.format(accuracy_score(y_test , mypredictions)))Dummy Classifier의 정확도는: 0.7877 정확도는 불균형한(imbalanced) 레이블 값 분포에서 ML 모델의 성능을 판단할 경우, 적합한 평가 지표 X
예를 들어 100개의 데이터(90개는 0, 10개는 1)를 무조건 0으로 예측 결과를 반환하는 모델의 경우 정확도가 90% 이다.
=> 평가의 지표로 정확도 사용 시 발생할 수 있는 문제점 (MNIST 데이터셋 활용)
1) MNIST 데이터셋을 multi classification에서 binary classification 으로 변경
: 0부터 9까지의 숫자 이미지의 픽셀 정보를 가지고 있음
: 이를 기반으로 숫자 Digit을 예측하는데 사용
: 사이킷런은 load_digits()를 API를 통해 MNIST 데이터셋 제공
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.base import BaseEstimator
from sklearn.metrics import accuracy_score
import numpy as np
import pandas as pd
class MyFakeClassifier(BaseEstimator):
def fit(self,X,y):
pass
# 입력값으로 들어오는 X 데이터 셋의 크기만큼 모두 0값으로 만들어서 반환
def predict(self,X):
return np.zeros( (len(X), 1) , dtype=bool)
# 사이킷런의 내장 데이터 셋인 load_digits( )를 이용하여 MNIST 데이터 로딩
digits = load_digits()
print(digits.data)
print('\n#digits.data.shape:', digits.data.shape)
print(digits.target)
print('\n#digits.target.shape:', digits.target.shape)
# 변형한 데이터의 분포도를 확인해보자
print('\n#레이블 테스트 세트 크기 :', y_test.shape)
print('\n#테스트 세트 레이블 0과 1의 분포도')
print(pd.Series(y_test).value_counts())[[ 0. 0. 5. ... 0. 0. 0.]
[ 0. 0. 0. ... 10. 0. 0.]
[ 0. 0. 0. ... 16. 9. 0.]
...
[ 0. 0. 1. ... 6. 0. 0.]
[ 0. 0. 2. ... 12. 0. 0.]
[ 0. 0. 10. ... 12. 1. 0.]]
#digits.data.shape: (1797, 64)
[0 1 2 ... 8 9 8]
#digits.target.shape: (1797,)
#레이블 테스트 세트 크기 : (179,)
#테스트 세트 레이블 0과 1의 분포도
0 110
1 69
Name: Survived, dtype: int642. 오차 행렬 (Confusion Matrix)
: 어떤 유형에 얼마나 오차가 있는지 보는 방법
: 암 환자 예측 예시에서의 설명
- TN : 실제 비 암환자를 비 암환자로 예측 건수
- FP : 실제 비 암환자를 암 환자로 예측 건수
- FN : 실제 암환자를 비 암환자로 예측 건수
- TP : 실제 암환자를 암환자로 예측 건수(해당 예제에서는 TP값이 매우 중요)
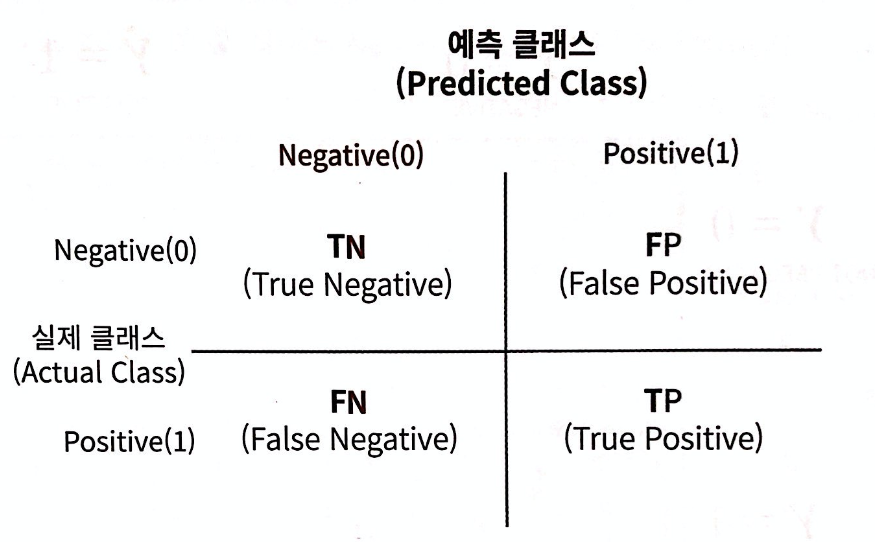
정확도 = 예측 결과와 실제 값이 동일한 건수 / 전체 데이터 수 = (TN+TP) / (TN + FP + FN + TP)
# 변형한 데이터의 분포도를 확인해보자
print('\n#레이블 테스트 세트 크기 :', y_test.shape)
print('\n#테스트 세트 레이블 0과 1의 분포도')
print(pd.Series(y_test).value_counts())#레이블 테스트 세트 크기 : (179,)
#테스트 세트 레이블 0과 1의 분포도
0 110
1 69
Name: Survived, dtype: int643. 정밀도 ( Precision ) & 재현율( Recall)
: Positive 데이터 세트의 예측 성능에 좀 더 초점을 맞춘 평가 지표입니다.
1) 정밀도
: 예측과 실제값이 Positive로 일치한 데이터의 비율
: FP + TP 는 예측을 Positive로 한 모든 데이터 건수이고 TP는 예측과 실제값이 Positive로 일치한 데이터 건수
: Positive 예측 성능을 더욱 정밀하게 측정하기 위한 평가 지표로 양성 예측도라고도 불림
TP / (FP + TP)
2) 재현율
: 실제 값이 Positive 인 대상 중 예측과 실제값ㅇ니 positvie 로 일치한 데이터의 비율
: FN + TP 는 실제값이 Positive인 모든 데이터 건수, TP는 예측과 실제값이 Positive로 일차한 데이터 건수
: 민감도(Sensitivity) 또는 TPR(True Positive Rate)라고도 불림
TP / (FN + TP)
- 재현율이 상대적으로 더 중요한 지표인 경우는? 실제 양성인 데이터 예측을 음성으로 잘못 판단하면 업무상 큰 영향이 발생한다.
ex) 암 판단, 보험사기, 금융사기 등
- 정밀도가 상대적으로 더 중요한 지표인 경우는? 실제 음성인 데이터 예측을 양성으로 잘못 판단하게 되면 업무상 큰 영향이 발생하는 경우
ex) 스팸메일 여부 판단 모델
- 재현율과 정밀도 모두 TP를 높이는데 동일하게 초점을 맞추지만,
: 재현율은 FN(실제 P, 예측 N)을 낮추는데 집중
: 정밀도는 FP(실제 N, 예측 P)를 낮추는 데 집중
: 서로 보완적인 지표로 분류의 성능을 평가하는데 적용
# 오차행렬, 정확도, 정밀도, 재현율을 한꺼번에 계산하는 함수 생성
from sklearn.metrics import accuracy_score, precision_score , recall_score , confusion_matrix
def get_clf_eval(y_test , pred):
confusion = confusion_matrix( y_test, pred)
accuracy = accuracy_score(y_test , pred)
precision = precision_score(y_test , pred)
recall = recall_score(y_test , pred)
print('\n#오차 행렬')
print(confusion)
print('\n#정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f}'.format(accuracy , precision ,recall))
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import warnings
warnings.filterwarnings('ignore')
# 원본 데이터를 재로딩, 데이터 가공, 학습데이터/테스트 데이터 분할.
titanic_df = pd.read_csv('C:\/train.csv')
y_titanic_df = titanic_df['Survived']
X_titanic_df= titanic_df.drop('Survived', axis=1)
X_titanic_df = transform_features(X_titanic_df)
X_train, X_test, y_train, y_test = train_test_split(X_titanic_df, y_titanic_df, \
test_size=0.20, random_state=11)
lr_clf = LogisticRegression(solver='liblinear')
lr_clf.fit(X_train , y_train)
pred = lr_clf.predict(X_test)
get_clf_eval(y_test , pred)#오차 행렬
[[108 10]
[ 14 47]]
#정확도: 0.8659, 정밀도: 0.8246, 재현율: 0.7705
3) 정밀도/재현율 트레이드오프
: 정밀도와 재현율의 지표는 상호보완적인 관계이기 때문에, TP값을 늘리는게 아닌 다른 F 지표를 강제로 낮추려고 할때, 다른 지표의 수치가 감소하게 된다.
: 이때, 분류 결정 임곗값을 조절해 정밀도와 재현율의 수치를 조정할 수 있다.
pred_proba = lr_clf.predict_proba(X_test)
pred = lr_clf.predict(X_test)
print('pred_proba()결과 Shape : {0}'.format(pred_proba.shape))
print('pred_proba array 에서 앞 3개만 샘플로 추출 \n:', pred_proba[:3])
pred_proba_result = np.concatenate([pred_proba, pred.reshape(-1, 1)], axis=1)
print('두 개의 클래스 중에서 더 큰 확률을 클래스 값으로 예측 \n', pred_proba_result[:3])pred_proba()결과 Shape : (179, 2)
pred_proba array 에서 앞 3개만 샘플로 추출
: [[0.44935225 0.55064775]
[0.86335511 0.13664489]
[0.86429643 0.13570357]]
두 개의 클래스 중에서 더 큰 확률을 클래스 값으로 예측
[[0.44935225 0.55064775 1. ]
[0.86335511 0.13664489 0. ]
[0.86429643 0.13570357 0. ]]: 이때 원래 사용했던 predict() 함수 같은 경우에는 예측을 해서 0,1 의 값으로 반환을 했지만 pred_proba_result() 는 다음과 같이 각 숫자에 대한 확률을 반환한다.
: 따라서 현재는 0,1 에 대한 구분이 0.5로 설정되어있지만 분류 결정 임곗값을 높이거나 낮춰서 정밀도와 재현율의 값을 조정할 수 있다.
4) Binarizer 클래스
# 이해를 돕기위한 Binarizer 예제
from sklearn.preprocessing import Binarizer
X = [[1, -1, 2],
[2, 0 , 0],
[0, 1.1, 1.2]]
# X의 개별 원소들이 threshold 값보다 같거나 작으면 0, 크면 1
binarizer = Binarizer(threshold=1.1)
print(binarizer.fit_transform(X))[[0. 0. 1.]
[1. 0. 0.]
[0. 0. 1.]]: 해당 평가지표는 타이타닉 데이터로 학습된 로지스틱 회귀 Classifier 객체에서 호출된 predict로 계산된 지표 값과 일치
-> predict 가 predict_probe에 기반함을 알 수 있
custom_threshold = 0.5
# predict_proba() 반환값의 두 번째 칼럼, 즉 positive 클래스 칼럼 하나만 추출해 Binarizer를 적용
pred_proba_1 = pred_proba[:, 1].reshape(-1, 1)
binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_1)
custom_predict = binarizer.transform(pred_proba_1)
get_clf_eval(y_test, custom_predict)오차 행렬
[[108 10]
[ 14 47]]
정확도 : 0.8659, 정밀도 : 0.8246, 재현율 : 0.7705, F1 : 0.7966Q. 임계값을 낮추면 어떻게 될까 ?
# Binarizer의 threshold 설정값을 0.4로 설정함
custom_threshold = 0.4
pred_proba_1 = pred_proba[:,1].reshape(-1,1)
binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_1)
custom_predict = binarizer.transform(pred_proba_1)
get_clf_eval(y_test, custom_predict)임곗값이 0.5에서 0.4로 낮아지면서 TP가 48에서 51로 늘고 FN이 13에서 10으로 줄었다.
이에따라, 재현율이 0.7869에서 0.8361로 좋아졌다. 하지만 FP는 14에서 20으로 늘면서 정밀도가 0.7742에서 0.7183으로 나빠졌고 정확도도 0.8492에서 0.8324로 나빠졌다.
-> 임계값을 낮추니, 재현율이 올라가고 정밀도가 떨어졌다.
이번에는 임곗값을 0.4에서부터 0.6까지 0.05씩 증가시키면서 평가 지표를 조사해보자.
thresholds = [0.4, 0.45, 0.5, 0.55, 0.6]
def get_clf_eval(y_test, pred):
confusion = confusion_matrix(y_test, pred)
accuracy = accuracy_score(y_test, pred)
precision = precision_score(y_test, pred)
recall = recall_score(y_test, pred)
print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f}'.format(accuracy, precision, recall))
def get_eval_by_threshold(y_test, pred_proba_c1, thresholds):
# thresholds list 객체 내의 값을 차례로 iteration하면서 evaluation 수행
for custom_threshold in thresholds:
binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_c1)
custom_predict = binarizer.transform(pred_proba_c1)
print(f'임곗값: {custom_threshold}')
get_clf_eval(y_test, custom_predict)
get_eval_by_threshold(y_test, pred_proba[:, 1].reshape(-1, 1), thresholds)임곗값: 0.4
정확도: 0.8212, 정밀도: 0.7042, 재현율: 0.8197
임곗값: 0.45
정확도: 0.8547, 정밀도: 0.7869, 재현율: 0.7869
임곗값: 0.5
정확도: 0.8659, 정밀도: 0.8246, 재현율: 0.7705
임곗값: 0.55
정확도: 0.8715, 정밀도: 0.8654, 재현율: 0.7377
임곗값: 0.6
정확도: 0.8771, 정밀도: 0.8980, 재현율: 0.7213
precision_recall_curve( )
: 임곗값 변화에 따른 평가 지표를 알아 볼 수 있는 API 제공
- 입력 파라미터
- y_true : 실제 클래스 값 배열 ( 배열 크기 = [데이터 건수])
- probas_pred : Positive 칼럼의 예측 확률 배열 ( 배열 크기 = [데이터 건수])
- 반환값
- 정밀도 : 임곗값 별 정밀도 값을 배열로 반환
- 재현율 : 임곗값 별 재현율 값을 배열로 반환
from sklearn.metrics import precision_recall_curve
# 레이블 값이 1일 때의 예측 확률 추출
pred_proba_class1 = lr_clf.predict_proba(X_test)[:, 1]
# 실제값 데이터 세트와 레이블 값이 1일 때의 예측 확률을 precision_recall_curve 인자로 입력
precision, recalls, thresholds = precision_recall_curve(y_test, pred_proba_class1)
print(f'반환된 분류 결정 임곗값 배열의 shape: {thresholds.shape}')
# 반환된 임곗값 배열 로우가 147건이므로 샘플로 10건만 추출하되, 임곗값을 15 step으로 추출
thr_index = np.arange(0, thresholds.shape[0], 15)
print(f'샘플 추출을 위한 임곗값 배열의 index 10개: {thr_index}')
print(f'샘플용 10개의 임곗값: {np.round(thresholds[thr_index], 2)}')
# 15 step 단위로 추출된 임곗값에 따른 정밀도와 재현율 값
print(f'샘플 임곗값별 정밀도: {np.round(precision[thr_index], 3)}')
print(f'샘플 임곗값별 재현율: {np.round(recalls[thr_index], 3)}')반환된 분류 결정 임곗값 배열의 shape: (165,)
샘플 추출을 위한 임곗값 배열의 index 10개: [ 0 15 30 45 60 75 90 105 120 135 150]
샘플용 10개의 임곗값: [0.02 0.11 0.13 0.14 0.16 0.24 0.32 0.45 0.62 0.73 0.87]
샘플 임곗값별 정밀도: [0.341 0.372 0.401 0.44 0.505 0.598 0.688 0.774 0.915 0.968 0.938]
샘플 임곗값별 재현율: [1. 1. 0.967 0.902 0.902 0.902 0.869 0.787 0.705 0.492 0.246]5) 정밀도와 재현율의 시각화
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
%matplotlib inline
def precision_recall_curve_plot(y_test, pred_proba_c1):
#threshold ndarray와 이 threshold에 따른 정밀도, 재현율 ndarray 추출
precisions, recalls, thresholds = precision_recall_curve(y_test, pred_proba_c1)
#X축을 thresholds, y축 정밀도, 재현율 값으로 각각 plot 수행, 정밀도는 점선으로 표시
plt.figure(figsize=(8,6))
threshold_boundary = thresholds.shape[0]
plt.plot(thresholds, precisions[0:threshold_boundary], linestyle='-', label='precision')
plt.plot(thresholds, recalls[0:threshold_boundary], label='recall')
#threshold 값 X축의 Scale을 0.1 단위로 변경
start, end = plt.xlim()
plt.xticks(np.round(np.arange(start, end, 0.1), 2))
#x축, y축 label과 legend, 그리고 grid 설정
plt.xlabel('Threshold value');plt.ylabel('Precision and Recall value')
plt.legend();plt.grid()
plt.show()
precision_recall_curve_plot(y_test, lr_clf.predict_proba(X_test)[:,1])
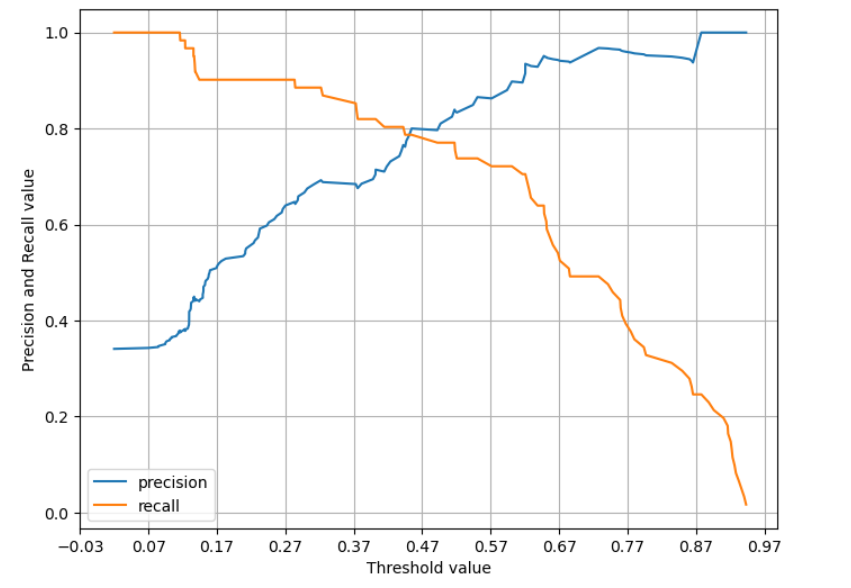
#파이썬머신러닝완벽가이드3장평가
'Data > 머신러닝' 카테고리의 다른 글
| [파이썬머신러닝완벽가이드]04.분류(1) (0) | 2023.05.20 |
|---|---|
| [파이썬머신러닝완벽가이드]03.평가(2) (0) | 2023.05.13 |
| [파이썬머신러닝완벽가이드]02.사이킷런으로 시작하는 머신러닝(2) (0) | 2023.04.28 |
| [파이썬머신러닝완벽가이드]02.사이킷런으로 시작하는 머신러닝(1) (0) | 2023.04.20 |
| [파이썬머신러닝완벽가이드]01.파이썬 기반의 머신러닝과 생태계 이해: 판다스 (1) | 2023.04.15 |



